Synthesis of 13C-depleted organic matter from CO in a reducing early Martian atmosphere

CO₂ photolysis experiment

Photolysis experiments were carried out in a glass flask apparatus with a UV-grade synthetic quartz window used in ref. ¹⁶. The diameter of the UV window was 3.6 cm. The volume of the apparatus was 448 cm³, and maximum path length was 13 cm. A Xenon arc lamp (Cermax, CX-04E, PE300BUV) was used as the UV source. The actinic UV spectrum was measured by a vacuum UV monochromator system⁴⁴ (Extended Data Fig. 1), which was used for calculating theoretical fractionation factor for the CO₂ photolysis.

Before the experiment, the glass flask was evacuated to below 0.1 Pa for more than 12 h. After evacuation, high-purity CO₂ (>99.99995%, Japan Air Gases) was introduced into the flask through the vacuum line to avoid contamination with air. The total gas pressure in the flask was measured using a capacitance manometer (MKS Baratron 626 B, 1–10 kPa range).

UV irradiation was performed at an output power of 20 A for the Xe lamp. The temperature of the flask was maintained at 315 ± 5 K using a cooling bath (AsOne MC-1). Before and during irradiation, a small aliquot of gas in the flask was sampled by expanding it to a calibrated volume with a syringe port. Each sample contained 1.7% of the total gas in the flask.

Carbon isotope analysis

The carbon isotopic composition of CO was measured using gas chromatography-combustion-isotope ratio mass spectrometry. The sampled gas was first purified by gas chromatography (Trace GC Ultra, Thermo Fisher Scientific) equipped with a capillary column (HP-MOLSIEVE:30 m × 0.53 mm i.d., 25 µm film thickness; Varian) to separate N₂, O₂, CO, CH₄ and CO₂. Ultra-high-purity He (>99.99995%, Japan Air Gases) was used as the carrier gas. The gas chromatography (GC) oven was maintained at 50 °C with a flow rate of 1.5 ml min⁻¹. After the analysis, the GC temperature was raised to 200 °C to remove any remaining gases in the column. Purified CO was then converted into CO₂ at 1,100 °C in a combustion furnace consisting of a ceramic tube packed with CuO, NiO and Pt wires. Then, CO₂ was introduced into an isotope ratio mass spectrometer (MAT253, Thermo Fisher Scientific) via the combustion furnace and continuous flow interface (GC Combustion III, Thermo Fisher Scientific). Isotopic standardization was performed using CO₂ injections calibrated against the National Institute of Standards and Technology natural gas standard, NGS-2.

Carbon isotope ratio is reported using the delta notation:

where ¹³R_CO and ¹³R_CO2 represent ¹³C/¹²C ratios of the sampled CO and the initial CO₂ used in the experiment, respectively. The initial CO₂ used in the photolysis experiment was also measured using GC-isotope ratio mass spectrometry (IRMS), as described in ref. ⁴⁵. On the basis of replicated analyses of the samples and in-house standard CO gas, the reproducibility of the measured δ¹³C–CO value was better than ±0.5‰. All the experimental results are summarized in Extended Data Tables 1 and 2.

Theoretical calculation for absorption cross sections for ¹²CO₂ and ¹³CO₂

The absorption cross sections for ¹²C¹⁶O¹⁶O, ¹³C¹⁶O¹⁶O and three other isotopologues of CO₂ were calculated from first principles using a time-dependent quantum mechanical methodology. The calculations were based on potential energy surfaces for the ground and lower excited states of CO₂, which were calculated using the multireference configuration interaction plus the Davidson correction to correlation energy (MRCI + Q) quantum chemistry method (ref. ¹⁷ provides details). The absorption cross sections for ¹²C¹⁶O¹⁶O, ¹³C¹⁶O¹⁶O, and three other isotopologues of CO₂ between 120 K and 395 K are available in the supporting information of ref. ¹⁷, in which Dataset S1 is for ¹²C¹⁶O¹⁶O, S2 is for ¹²C¹⁶O¹⁷O, S3 is for ¹²C¹⁶O¹⁸O, S4 is ¹³C¹⁶O¹⁶O and S5 is for ¹³C¹⁶O¹⁸O.

Calculation of the fractionation factor for CO₂ photolysis in the experiment

In the CO₂ photolysis experiment, carbon isotope fractionation potentially originates from the following two reactions:

where M represents the third-body reaction partner. The reaction rates of reactions (R1) and (R2) are proportional to the number densities of CO₂ and CO and thus can be written as J[CO₂] and k’[CO], respectively. In our experiment, more than 99.7% of CO₂ remained in the system, and thus the reaction rate of reaction (R1) (that is, J[CO₂]) was constant, whereas the reaction rate of (R2) (that is, k’[CO]) increased in response to elevated [CO] (Fig. 2). In this case, the isotopic fractionation factors for (R1) and (R2) are defined as

where ¹²J and ¹³J are the photolysis rate coefficients of ¹²CO₂ and ¹³CO₂, respectively. In addition, ¹²k’ and ¹³k are the rate constants for ¹²CO and ¹³CO, respectively. The J, k’, α₁ and α₂ values were estimated by fitting the observed changes in CO / (CO + CO₂) and δ¹³C–CO (Fig. 2).

For the 33-kPa experiment (Extended Data Table 1), the best fit values for J and k’ were 4.3 × 10⁻⁷s⁻¹ and 1.7 × 10⁻⁴s⁻¹, respectively. The steady-state CO/CO₂ ratio (= J / k’) was 0.0025. In reality, a longer experiment yields O₂ via the following reaction.

When O₂ accumulates in the system, the simple assumptions above are no longer applicable owing to the more complex O₂ photochemistry and UV shielding by O₂, both of which should affect the k’ and J values. Therefore, we report the data only before O₂ accumulated in the system (up to 4 h under our experimental conditions).

In addition, the same model simulation was performed by splitting the J and k values into those for ¹²C and ¹³C species by assuming fractionation factors α₁ and α₂. For the 33-kPa experiment (Extended Data Table 1), the best fit values for α₁ and α₂ were 0.871 ± 0.001 and 1.0074 ± 0.0005, respectively. Consequently, the observed isotope fractionation (δ¹³C–CO from −133‰ to −121‰) is largely due to the isotope effect of CO₂ photolysis (1,000 ln α₁ = −138 ± 1‰) with a smaller contribution from reaction (R2) (1,000 ln α₂ = +7.4 ± 0.5‰).

To confirm the small isotope effect of reaction (R2), additional experiments were performed, in which the reaction rate of reaction (R2) was enhanced by adding O₂ (Extended Data Table 2). In this experiment, a 1:2:8 mixture of CO:O₂:N₂ was photolysed using the same UV source. After 345 min, 30% of the initial CO was consumed via reaction (R2). The remaining CO showed a relatively large scatter in its δ¹³C value (±4.4‰; n = 8) and did not show a significant correlation with the remaining CO fraction. These results confirmed that the isotope effect of reaction (R2) should be smaller than ±13‰ when considering a possible ±4.4‰ change at 30% consumption. This is consistent with the estimated +7.4 ± 0.5‰ isotope effect for reaction (R2).

In an actual atmosphere, photolysis generates oxygen atoms (O), although the direct recombination of CO with O to give CO₂ is forbidden by the conservation of spin and is therefore very slow, allowing quantitative amount of CO to build up⁴⁶. The excess oxygen is removed by the oxidation of surface minerals or escapes into space, and the atmosphere overall could be weakly reducing.

Also, in actual atmosphere, presence of H₂O may change the photochemistry relative to our dry experimental condition. Photodissociation of H₂O creates the OH radical, which is the dominant oxidant of CO. Therefore, in wet conditions, CO oxidation rate is faster than in a dry atmosphere^13,14,15,16. On the other hand, the presence of H₂O does not change the fractionation factor of CO₂ photolysis (α₁) unless water vapour considerably modifies the actinic UV spectra. The spectral effect is evaluated in the following sections.

Comparison to theoretical fractionation factor in the experimental condition

The observed large isotope effect in CO₂ photolysis (α₁ = 0.871 ± 0.001; 1,000 ln α₁ = −138 ± 1‰) was compared with theoretical calculations to obtain a mechanistic understanding of this effect. Theoretically, the isotopic fractionation factor for CO₂ photolysis (α₁) can be calculated using equation (1) and absorption cross sections for CO₂ isotopologues¹⁷

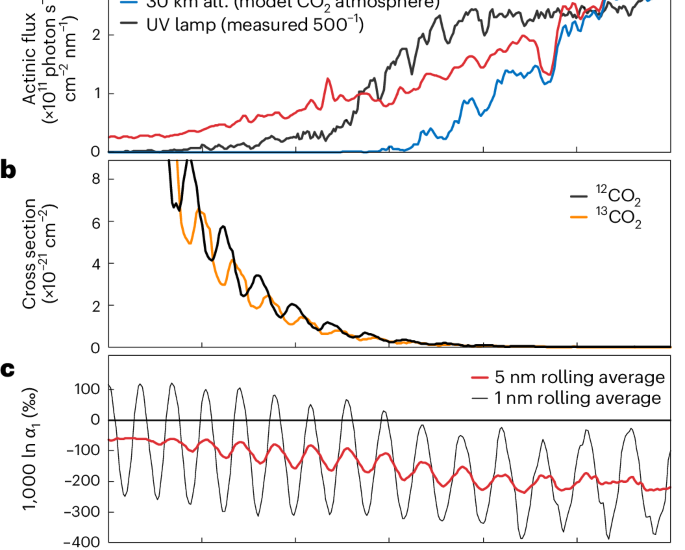
where ¹²J and ¹³J represent the photolysis rate coefficients of ¹²CO₂ and ¹³CO₂, respectively. φ(λ) is the quantum yield, which is assumed to be unity in the integral range from 170 nm to 210 nm. ¹²σ(λ) and ¹³σ(λ) are absorption cross sections at a wavelength λ for ¹²CO₂ and ¹³CO₂, respectively, as reported in ref. ¹⁷. I(λ) is the incident UV spectrum in our experimental condition, measured by the vacuum UV monochromator used in ref. ³⁵ (Extended Data Fig. 1). The opacity term τ(λ) was calculated as follows:

where σ_i(λ) is the absorption cross section of the UV-shielding molecule i and \(\int {\rho }_{i}(z)dz\) represents the column density of molecule i in path length z. The gases defining the opacity term should have large cross sections in the 170–210 nm wavelength range. Potentially, the presence of O₂ and CO₂ (self shielding) can change the actinic UV flux, thereby changing the fractionation factor α₁.

The calculation results are summarized in Extended Data Fig. 1. First, the actinic UV spectra did not change considerably from the front and rear ends of the 13-cm-long apparatus (Extended Data Fig. 1). CO₂ self shielding may shift the isotope effect (1,000 ln α₁) by up to −1‰ for 33-kPa CO₂ and by a negligible amount for 10 kPa CO₂ (Extended Data Fig. 1). UV shielding by O₂ may possibly cause a larger shift of up to −4‰, even considering an improbably high O₂ content (100 Pa; Extended Data Fig. 1). In our experiment, O₂ was formed by reaction (R3), although its concentration was probably lower than that of CO (maximum 70 Pa: Extended Data Table 1). Conservatively, we take ±4‰ as the error derived from the uncertainty of the UV spectrum.

The uncertainty arising from temperature may cause a larger variation. Although our UV experiment started at 297 K, the temperature increased to 315 ± 5 K after 10 min. The heating of the apparatus was inevitable in the current experimental setting. On the other hand, the ab initio cross sections for the CO₂ isotopologues change slightly depending on temperature¹⁷. Using the cross sections at 295 K, the estimated isotope effect (1,000 ln α₁) was 9.4‰ larger than that using 320 K cross sections (Extended Data Fig. 1). We found that a lower temperature resulted in larger fractionation (in other words, a more negative 1,000 ln α₁ value) with a slope of +0.51‰ K⁻¹ from 220 K to 320 K.

Considering the above uncertainties, the theoretical fractionation factor α₁ for our experimental condition (33 kPa CO₂) was 0.845 ± 0.004, corresponding to −168 ± 5‰ for 1,000 ln α₁, which was 30‰ more negative than the observed isotope effect of −138 ± 1‰.

The systematic 30‰ difference may not be due to uncertainties in the UV experiment, but are more likely due to inaccuracies in the ab initio potential energy surfaces used to calculate the theoretical CO₂ cross sections. Precise calculations in the lower energy region of the absorption cross section are particularly difficult. On the basis of the ¹²J and ¹³J spectra (Extended Data Fig. 1), the lower energy part (that is λ > 183 nm) is the main region giving rise to large fractionation. Considering the difficulty of the calculation, a conservative estimate of the error in the ab initio cross sections is ±50‰, which is similar to the theoretical fractionations calculated for similar gases, including nitrous oxide (N₂O)⁴⁷ and carbonyl sulfide (OCS)⁴⁸. Therefore, we estimate that the experimentally determined isotope effect (−138 ± 1‰) is consistent with the theoretical fractionation within an uncertainty of ±50‰. Note that calculated fractionation using theoretical cross sections¹⁷ overestimates fractionation by 30‰ relative to the experiment. The ab initio calculation and the experiment confirm our hypothesis that broadband UV photolysis of CO₂ is associated with a large negative carbon isotope effect in excess of −100‰.

Estimated fractionation factor for CO₂ photolysis in the early Mars atmosphere

In the early Martian atmosphere, the isotope effect in CO₂ photolysis was larger than that observed in the laboratory. Considering the above fractionation mechanism, isotopic fractionation changes depending on the following key parameters:

1. 1.

   Temperature

2. 2.

   Actinic UV spectrum

3. 3.

   UV shielding by atmospheric species

All three of these factors from the early Mars were different from the experimental conditions and are not precisely known. Therefore, we built a 1D atmospheric simulation model to help understand the sensitivity and error.

The base model assumed a hydrostatic CO₂ atmosphere with 10 mbar P_CO2 at the surface (Extended Data Fig. 2a). The vertical temperature profile had a temperature of 240 K at the surface (dashed line in Extended Data Fig. 2a), which agrees with observations of the current Martian atmosphere⁴⁹. A warmer case (300 K at the surface) was also calculated in the model (solid line in Extended Data Fig. 2a) to simulate early Mars with liquid water present on the surface.

The actinic UV spectra were calculated assuming the solar UV spectrum from ref. ⁴³ and UV attenuation by CO₂ at each altitude (Extended Data Fig. 2d). The UV scattering by CO₂ was also considered using the scattering cross section from ref. ⁵⁰.

The photolysis rates for ¹²CO₂ and ¹³CO₂ were calculated using equations (3), (4) and (5) (Extended Data Figs. 2b,e), which gives the isotopic fractionation factor (α₁) at each altitude from equation (1) (Extended Data Fig. 2c). To evaluate the temperature dependence, we used ¹²CO₂ and ¹³CO₂ cross sections at each temperature of the altitude profile¹⁷. A lower temperature results in a larger calculated fractionation with a slope of +0.8‰ K⁻¹, which is similar to, but slightly steeper than, that obtained under experimental conditions using a Xe lamp as a UV source ( + 0.5‰ K⁻¹). Considering the systematic shift from theoretical to experimental fractionation observed, the 1,000 ln α₁ value was corrected with a + 30‰ shift across the temperature range.

Estimated carbon isotope ratio for volcanic CO₂ and CO of Mars

We employed a δ¹³C value of −25 ± 5‰ for mantle-derived volcanic CO₂ and CO (Fig. 3). This value was derived from stepwise heating experiments of shergottite–nakhlite–chassignite (SNC) meteorites⁵¹. Because SNC meteorites are igneous rocks that are interpreted to represent either lavas or plutonic cumulates⁵², high-temperature releases of SNC meteorites would record magmatic volatiles. The high-temperature releases (>1,000 °C) of shergottites (basalt: Shergotty and Zagami), nakhlites (clinopyroxenite: Nakhla, Lafayette, Governador Valadares) and chassignite (dunnite: Chassingy) yielded a limited δ¹³C range (−20‰ to −30‰), despite the fact that these meteorites have distinct formation and Mars ejection ages; that is, they were formed by different magmatic activities and were derived from different launching sites on Mars^53,54. The limited δ¹³C values (−20‰ to −30‰) suggest the existence of a common carbon reservoir in the Martian interior.

Estimated carbon isotope ratios for 4 Ga Mars surface water component and atmospheric CO₂

We employed a δ¹³C value of +30 ± 10‰ for the dissolved inorganic carbon component of 4 Ga surficial water. This value is derived from ~4 Ga carbonates contained in the Allan Hills (ALH) 84001 Martian meteorite^19,20,21. ALH 84001 is an igneous cumulate (orthopyroxenite) that experienced post-magmatic aqueous alteration, resulting in the precipitation of secondary phases including carbonate^55,56. Radiogenic isotope systematics (Lu–Hf, Pb–Pb and Rb–Sr) of this meteorite yield the magmatic crystallization age and the carbonate formation age of 4.09 ± 0.03 Ga and 3.9–4.0 Ga, respectively^57,58. Carbon and oxygen isotope studies indicate that carbonates were formed by distillation and loss of CO₂ from the fluid during evaporation and degassing^20,59 resulting in zoned isotopic enrichment of δ¹⁸O and δ¹³C from the core to the rim^{19,60,61,62,63}. Triple oxygen isotope analyses further implied that the CO₂ fluid could have been initially in equilibrium with the atmosphere^21,64. The δ¹³C value of +30 ± 10‰ employed in this study was determined to cover a reported δ¹³C range from 20‰ to 40‰ for Ca- and Fe-rich carbonates, which are interpreted as representing near-primary precipitates in ALH 84001 (ref. ²¹).

A notable feature of ALH 84001 is that the carbonates are accompanied by polycyclic aromatic hydrocarbons, nanocrystal magnetites and iron sulfides because their petrographic context and textures (for example, chain-like structure of magnetite similar to magnetotactic bacteria) invoked a possible sign of life on Mars. A question related to the biogenic origin of carbonate–magnetite–sulfide assemblages is whether they formed at a sufficiently low temperature that was suitable for life. A variety of formation temperatures from 0 °C to 650 °C have been proposed for the ALH 84001 carbonates^{19,20,59,60,61,62,63,65,66,67,68}, but recent stable isotopic studies including clumped isotope geothermometry have led to a consensus that the ALH 84001 carbonates formed in a low-temperature environment (~20 °C) (for example, ref. ²⁰). Although the low-temperature condition is consistent with both abiotic and biogenic origins, the carbonate–magnetite–sulfide assemblage in ALH 84001 is now explained as arising from abiotic processes (for example, thermal decomposition of iron carbonate due to impact-induced shock heating)^69,70.

Assuming isotopic equilibrium between carbonate and atmospheric CO₂ (1,000 ln α_{carbonate-CO2} = 9.8‰ at 25 °C; ref. ⁷¹), we employed a δ¹³C value of +20 ± 10‰ for atmospheric CO₂ on early Mars (Fig. 3).

Mass balance model

Carbon isotope ratios of atmospheric CO₂ (δ¹³C_CO2) and CO (δ¹³C_CO) were calculated based on the mass balance shown in Fig. 3c. In this simple mass balance model, we assume that the atmospheric CO₂ arises primarily from volcanic input (δ¹³C_CO2-i = −25 ± 5‰ as noted above) and removed as organics synthesized from CO. For simplicity, carbon isotopic fractionation (α) is assumed to occur only in the CO₂ photolysis. Then, isotopic compositions of atmospheric CO₂ is determined by remaining fraction (f) of CO₂ after the photolysis:

Owing to mass balance:

isotopic compositions of atmospheric CO is:

In this model, we do not consider carbon escape into space, which may also cause ¹³C enrichment of remaining CO₂. Therefore, the estimated f is regarded as the maximum value if a considerable fraction of the atmospheric CO₂ escapes into space. In addition, molecular diffusion in the upper part of the atmosphere may also cause isotopic fractionation. However, based on our more detailed atmospheric model³¹, this effect is important only above 100 km altitude, which accounts for less than 10⁻⁶ of total atmospheric CO₂. Therefore, it is reasonable to neglect the isotope effect of molecular diffusion in calculating the mass balance.

Note that the model does not consider further processes that fractionate isotopes after CO₂ photolysis (that is, α = α₁). Therefore, the isotopic composition of the organic matter (δ¹³C_org) is equal to that of atmospheric CO (δ¹³C_CO). This assumption may not be true if some organics were produced not from the CO but from the other carbon sources with normal or heavy isotopic composition. In a CO₂ and/or CO atmosphere, however, organic synthesis is initiated from the HCO radical produced by CO^{13,16,31,35,46,72,73,74,75}:

In comparison to reaction (R1), it is very likely that carbon isotope fractionations for reactions (R4)–(R6) are an order of magnitude smaller than the CO₂ photolysis^31,76,77. Therefore, it is reasonable to assume the strongly ¹³C-depleted signature in CO should be transferred to formaldehyde and other organics. There is no known atmospheric reaction that incorporates the isotopically normal CO₂ directly into organic molecules⁷⁷, unless CO₂ is photolysed into CO with a large isotopic fractionation (reaction (R1)). The possible alternative carbon source with normal ¹³C abundance is volcanic CO. Therefore, we have performed additional calculations considering 10%, 20% and 30% addition of volcanic CO (δ¹³C_CO-i = −25 ± 5‰) and shown in Fig. 3.