Wave-momentum shaping for moving objects in heterogeneous and dynamic media

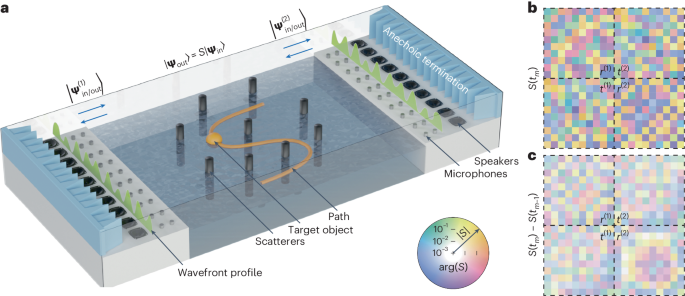
Experimental set-up

The set-up consists of a water-filled tank (Fig. 1a and Supplementary Fig. 1a) coupled at the top to a two-dimensional air waveguide terminated at both ends by anechoic terminations. The water tank’s width, length and height are 100 × 100 × 3 cm, respectively. The two-dimensional acoustic waveguide above it has a width of 104 cm, a length of 180 cm and a height of 8 cm. Two columns of ten microphones (ICP 130F20, 1/4 inch, PCB Piezotronics) separated by 5 cm were placed between the tank and the anechoic terminations on each side to measure the distribution of the complex pressure field inside the waveguide. Two columns of ten amplified loudspeakers (Monacor MSH-115, 4 inches, with in-house amplifiers) were placed horizontally on the bottom of each end of the air waveguide to ensure the efficient excitation of all ten modes inside the acoustic structure. The incident wave states were generated with a Speedgoat Performance Real-Time Target Machine controller (I/O 135, sampling rate 10 kHz) with 40 inputs and 20 outputs. The same equipment was used to acquire the corresponding far-field scattering. To generate the proper acoustic wavefronts, the controller was programmed by Matlab/Simulink to control the voltage of the 20 loudspeakers. The voltages produced by 40 microphones corresponding to the pressure signals were then acquired. Sensor conditioners (483C05, PCB Piezotronics) were used to precondition the microphone signals. Examples of captured signals and post-processing are shown in Supplementary Fig. 2.

The moving target scatterer was a ping-pong ball (diameter 4 cm and weight 4.17 g) floating on the water’s surface. The static disorder scatterers were plastic cylinders of various diameters (2 to 4 cm) immersed in the water tank. They extended above the surface but without reaching the upper part of the two-dimensional air waveguide. The cylinders and the ball were coated with candle wax (a hydrophobic film) to prevent the ball from sticking to the static scatterers by capillarity. The real-time position of the ball (Fig. 4) was captured by an ultra-wide webcam (Logitech Brio), working in full high-definition resolution (1,920 × 1,080 pixels) at a high refresh rate (60 frames per second). A small iron nut was glued to the moving target. It was placed at its initial (starting) position by using an electromagnet attached to a mechanical arm (Supplementary Fig. 1b), which was moved in a volume (1,000 × 1,000 × 110 mm) above the water tank by three high-precision linear stages (Newport IMS stages with displacement error <0.05 mm).

The rotating object shown in Fig. 3 comprised three ping-pong balls glued together in a line. A needle was fixed to the bottom of the tank, and the centre of the middle ball was impaled on the needle to prevent linear displacement of the object and allow only rotation while limiting friction. The three balls were painted with different patterns to facilitate the detection of the instantaneous angle.

To create the dynamic scattering medium, we used ten ping-pong balls and glued small metallic nuts onto them. The scattering balls, evenly positioned around the intended paths, were attached to the bottom of the water tank by 3- to 8-cm-long nylon threads. The random fluctuations of these scatterers were exacerbated by randomly moving the mechanical arm over the balls while randomly switching the state of the attached electromagnet. The disorder scatterers were placed at a significant enough distance from the target scatterer, which was still free-floating, to avoid any collisions.

Finally, the top plates above the water tank could be replaced with carefully designed perforated plates (holes with a diameter of 1 mm and forming a square array with a period of 10 mm; Supplementary Fig. 1e) to allow the field inside the waveguide to be scanned by a microphone placed on the robotic arm outside the waveguide.

Scattering matrix measurement

The complex scattering matrix S relates the incoming with the outgoing flux-normalized modes through a set of 2N linearly independent equations (2N = 20 is the total number of propagative modes, ten from each side): ψ_out = S ψ_in. Solving the scattering matrix S requires measuring N independent wave mode distributions excited by a combination of speakers that form an orthogonal basis. Our experiment uses an orthonormal basis, and only one speaker is excited at a time with the 1,590 Hz harmonic signal. For each excitation, the data collected by the microphone arrays on both sides can be used to determine the incident and outgoing modes ψ_in,out. With the hardware we used, this takes about 80 ms. Therefore, after 2N orthogonal excitations (1.6 s), the scattering matrix is solved for that particular scattering configuration. This type of raw scattering matrix is neither perfectly symmetric nor unitary and is subsequently regularized by discarding its very small antisymmetric part and rescaling its subunitary eigenvalues while keeping their phases (Supplementary Fig. 3).

Construction of GWS operators

The construction of the GWS operator Q_α is based on gradient approximations, which require successive measurements of the scattering matrix S(t) at three different positions (time).

To derive the translation GWS operators Q_x and Q_y for the ball at position (x_m, y_m) and time instance t_m, we need, in addition to the scattering matrix S_m measured at the actual position, the scattering matrices S_m−1 and S_m−2 measured at the two previous time instances t_m−1 and t_m−2, when the ball was at coordinates (x_m−1, y_m−1) and (x_m−2, y_m−2), respectively.

With these three matrices S_m, S_m−1 and S_m−2, the gradient of S can be derived with the following approximation formula:

With the gradient estimated, the construction of the GWS operators Q_x and Q_y is direct:

The error in the gradient approximation and, therefore, in the operators Q_x and Q_y, depends on the shape of the triangle formed by the three measurement points, with the best results obtained for an equilateral triangle and worse for a flat scalene one (Supplementary Fig. 6). A detailed analysis of the triangle’s influence on the derivation of the GWS operator is provided in Supplementary Information Section 6. Therefore, for the best manipulation of the object position, the path is drawn with a zigzag line to minimize the error in the GWS operators.

Similarly, the rotation GWS operator Q_θ requires the measurement of S_m, S_m−1 and S_m−2 for three consecutive vane angles θ_m, θ_m−1 and θ_m−2 taken at times t_m, t_m−1 and t_m−2.

The gradient approximation is, in that case, derived with a backward three-point derivative

where δθ is the angle difference between the time instances t_m and t_m−1.

The GWS operator constructed to control the rotation of the vanes, therefore, reads as follows

Injection of optimal input mode mixtures

As explained in the text, finding the optimal mode mixture to be injected to give the optimal momentum push to the object follows from equation (1). We, therefore, provide a short proof for this important equation.

For a particle in free space, the change of momentum transferred to it upon scattering Δp_α can be calculated from the expectation values of the operator C_α = −i∂/∂α for the superposition states \(\left\vert {{{{\boldsymbol{\Psi }}}}}_\mathrm{in,out}\right\rangle\)

We can then write:

Using S^†S = 1, we can write 〈Ψ_in∣d/dα∣Ψ_in〉 = 〈SΨ_in∣S d/dα∣Ψ_in〉 and obtain

The term in parentheses is nothing but \(\frac{\mathrm{d}S}{\mathrm{d}\alpha}\left\vert\mathbf{\Psi}_{{{{\mathrm{in}}}}}\right\rangle\), and we directly get

In refs. ^44,45, it was shown that equation (1) continues to hold, even when the target particle is embedded in a scattering environment. In this way, the momentum push expected for a given far-field input is expressed as the expectation value of the GWS operator Q_α, which is Hermitian. Therefore, the eigenvector of Q_α provides the optimal momentum push with the highest eigenvalue.

Having measured the Wigner–Smith operators, we diagonalize them and find the eigenvector with the highest eigenvalue. We use the eigenvalues to calculate the optimal mode mixture to be injected to give the optimal momentum push to the particle. For example, if we want to move the object by Δx and Δy: (1) We diagonalize Q_x and Q_y. (2) We obtain their eigenvectors with highest eigenvalues Ψ_x,y, with eigenvalues calculated as δx and δy. (3) We construct the optimal input state \(\frac{\Delta\, x}{\delta x}{\mathbf{\Psi}}_{x}+\frac{\Delta\, y}{\delta y}{\mathbf{\Psi}}_{y}\). This input state is multiplied by the coupling coefficient matrix of the speakers M to give the required voltage amplitudes and phases required on each speaker (Supplementary Figs. 2 and 5). In practice, to determine the direction we want to go, we measure the position of the ball (x, y) at a given time (Supplementary Fig. 4) and compare it with the position of the next checkpoint on the trajectory, which we try to reach up to a certain threshold distance before moving on to the next checkpoint.